Grammaires

Définition

Nous pouvons générer des mots grâce aux grammaires.

Une grammaire est composée de symboles terminaux appartenant à $\Sigma$ non terminaux auxquels on rattache des règles de production ces règles peuvent dériver vers des non terminaux pour appliquer leur règles. Une grammaire admet une règle de départ.

Par exemple avec la grammaire suivante sur $\Sigma =\{a,b\}$

S -> a
S -> a
S -> <epsilon>
S -> aSa
S -> bSb

On peut avoir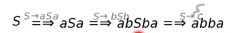

IMPORTANT

On définit donc une grammaire hors-contexte $G<A_N,\Sigma ,P,S>$ où on a:

• $A_N$ est l’ensemble des symboles non-terminaux
• $\Sigma$ un alphabet
• $P$ un ensemble de règles de la forme $X->a$ avec $X\in A_N$ et $a\in (A_N\cup \Sigma )\ast$
• $S\in A_N$ le symbole de début

NOTE

On parle de hors contexte car en gauche de règle il n’y a qu’un seul non-terminal et car les ce qui est autour d’un symbole non terminal n’est pas connu pendent la dérivation

Régularité à droite

Une grammaire régulière à droite est une grammaire dont les règles ont les terminaux à gauche et UN SEUL non terminal à droite, ce qui permet de faire un produit en quelque sorte car en dérivant on rajoute des lettres à droite du mot. On repasse donc le mot au fur et à mesure de sa génération comme le ferait un automate.

Nous pouvons voir chaque dérivation comme un changement d’état dans l’automate associé.

INFO

$Reg(\Sigma \ast )$ est l’ensemble des langages correspondant aux grammaires $Rec(\Sigma \ast )$ est l’ensemble des langages reconnaissable par un automate déterministe

IMPORTANT

Donc $Reg(\Sigma \ast )=Rec(\Sigma \ast )$ pour les grammaires régulières à droite