Fonction coût et Gradient descendant

Fonction coût

Quand on fait un modèle de machine learning on préfère que les erreurs dans les prédictions de nôtre modèle soient les plus petites possible. On utilise donc une fonction coût $J$, utilisant l’approche méthode des moindres carrés qui nous permet de quantifier l’écart entre les prévisions obtenues et les observations que l’on a eu pendant l’entraînement.

$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^i)-y^i{)}^2$

Brève explication

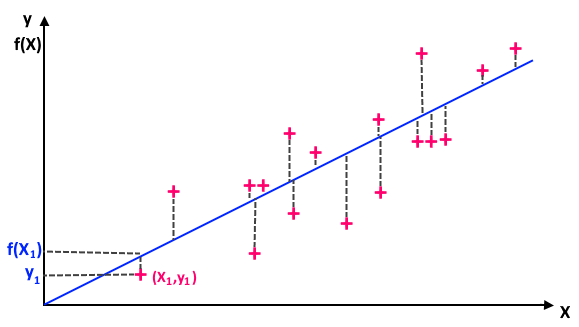
Elle [La fonction coût] permet d’ajuster un nuage de points (observations) représentés sur un plan (diagramme de dispersion) où l’axe des abscisses ($x$) représente la variable explicative et où l’axe des ordonnées ($y$) représente la variable expliquée. Le centre de gravité de ce nuage est représenté par le point dont les coordonnées sont (moyenne des $x_i$, moyenne des $y_i$). La méthode des moindres carrés consiste à rechercher la relation affine qui lie les variables $x$ et $y$; ce qui revient à définir l’équation de la droite du type $y=ax+b$, qui passe le plus près possible de tous les points, autrement dit qui [minimise l’écart et donc les erreurs].

Ci-dessous un tracé de $h_{\theta }(x)$

- https://franckybox.com/fonctions-de-cout-et-machine-learning/

TLDR

$J$ représente la somme des erreurs au carré du modèle pour toutes les features $x^i$, le résultat attendu étant $y^i$ et le résultat donné par le modèle $h_{\theta }(x^i)$

Gradient Descendant

L’algorithme de gradient descendant est un algorithme itératif permettant de trouver les paramètres tel que la fonction coût $J$ donne le résultat le plus petit possible. On va chercher à converger vers le minimum de $J$.

L’algorithme marche en dérivant $J$ sur un point $p$ plusieurs fois et en avançant dans $J$ en fonction:

• Si la dérivée de $j$ sur $p$ aka la step size est faible alors on approche du minimum de $J$, on va donc faire un petit pas.
• Si la step size est importante alors le minimum de $J$ (donc du taux d’erreur est importante) est loin, on va donc faire un grand pas.

Sauf que notre saut pourrait être trop grand au point d’avoir une erreur plus importante.

On va donc définir que: $stepsize=\alpha \times \frac{\delta J(\theta )}{\delta \theta }$ Soit $\alpha$ un réel positif très petit appelé le learning rate, réduisant le saut.

On arrête l’algorithme quand la dérivée sur $p$ est plus petite que le learning rate.

IMPORTANT

Plus $\alpha$ est petit plus nos sauts seront précis mais la convergence prendra du temps en échange

Vidéo d'illustration