Quand un développeur crée un programme, il part du principe que ses variables dans la heap ou une stack, tous deux situés dans la mémoire de l’ordinateur (généralement de la RAM), Il est donc normal de penser que son programme exécuté par le processeur écrit et lit directement dans la mémoire.
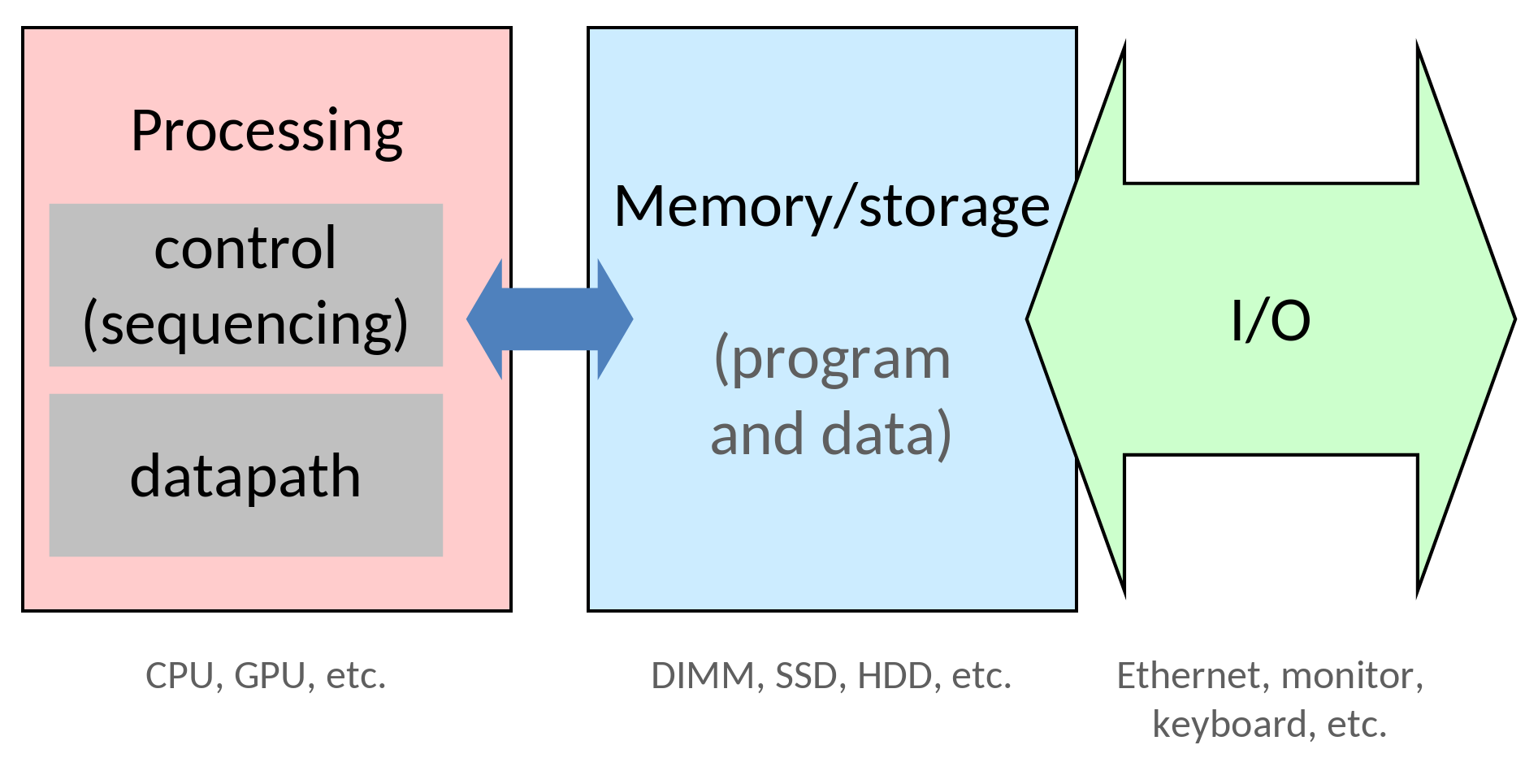
Cependant il y a un hic: l’exécution d’instruction et accès à la mémoire ne se font pas instantanément, cela prend un certain nombre de cycles pour se faire.
Les sticks de RAM les plus courants pouvant aller jusqu’à 16 ou 32 Go (soit octets) comment faire pour accéder à cet océan de données si vite ? Avec des caches !
Les caches
En réalité le processeur de notre développeur ne passe pas directement dans la RAM, son programme passe d’abord par des caches qui fait l’intermédiaire entre le datapath et la mémoire. Les processeurs contiennent caches L (L pour Layer), en général il y en a 2 ou 3, avoir plusieurs caches placés les uns à la suite des autres permet d’avoir l’illusion d’avoir une mémoire aussi large que la RAM et aussi rapide que le cache L1 (ce qu’on appelle la mémoire virtuelle en opposition à la mémoire physique qu’est le le stick de RAM).
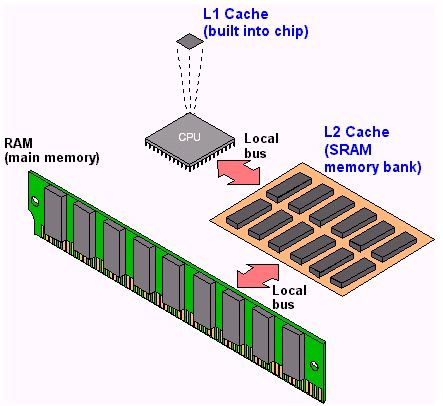
En général les caches sont très utiles pour gérer les deux principes de localité :
- La localité spatiale: Désigne un programme qui accède souvent à une certaine région de mémoire (ex: les arrays)
- La localité temporaire: Désigne un programme qui accède souvent à la même adresse mémoire en un temps court (ex: les boucles)
Calculer le temps d’accès à un cache
Soit :
- le temps d’accès (en cycles) à la mémoire de niveau
- le hit rate au niveau , concrètement la chance que la donnée soit à ce niveau
- le miss rate au niveau , concrètement la chance que la donnée ne soit à ce niveau
On définit le nombre de cycles pour accéder à une donnée ainsi, exemple avec allant jusqu’à 2:
On peut résumer la formule à celle-ci:
Fonctionnement d’un cache
Direct-mapped cache
Quand on va accéder à un cache on va d’abord aller dans un tag store pour vérifier si la donnée se trouve dans le cache, si ce n’est pas le cas on passe au cache suivant (ou à la mémoire), sinon on lit le dans le data store qui contient notre valeur recherchée.
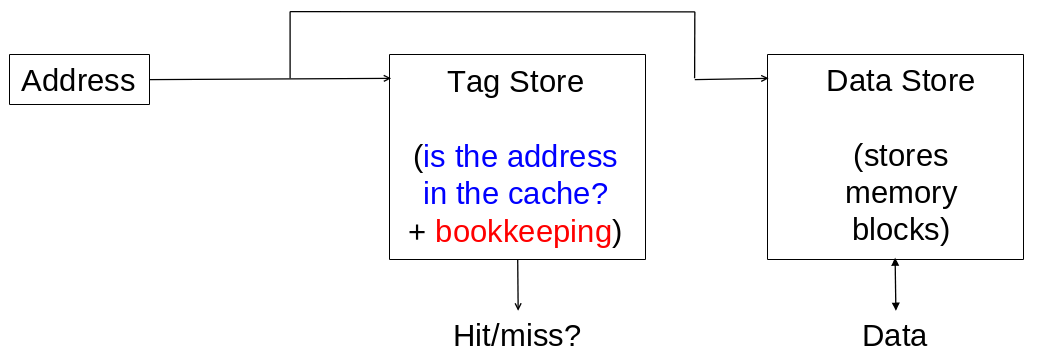
Les adresses sont sur 8 bits, quand on utilise les adresses dans le cadre d’un cache l’adresse correspond aux coordonnées dans le tag store.
| Tag | Index | Block |
|---|---|---|
| 2 bits | 3 bits | 3 bits |
| Si il est égal à ce qui est stocké dans la ligne du tag store on a un cache hit | Définit la ligne du bloc ciblée et la ligne dans laquelle regarder le tag dans le tag store | Bloc de mémoire dans lequel regarder |
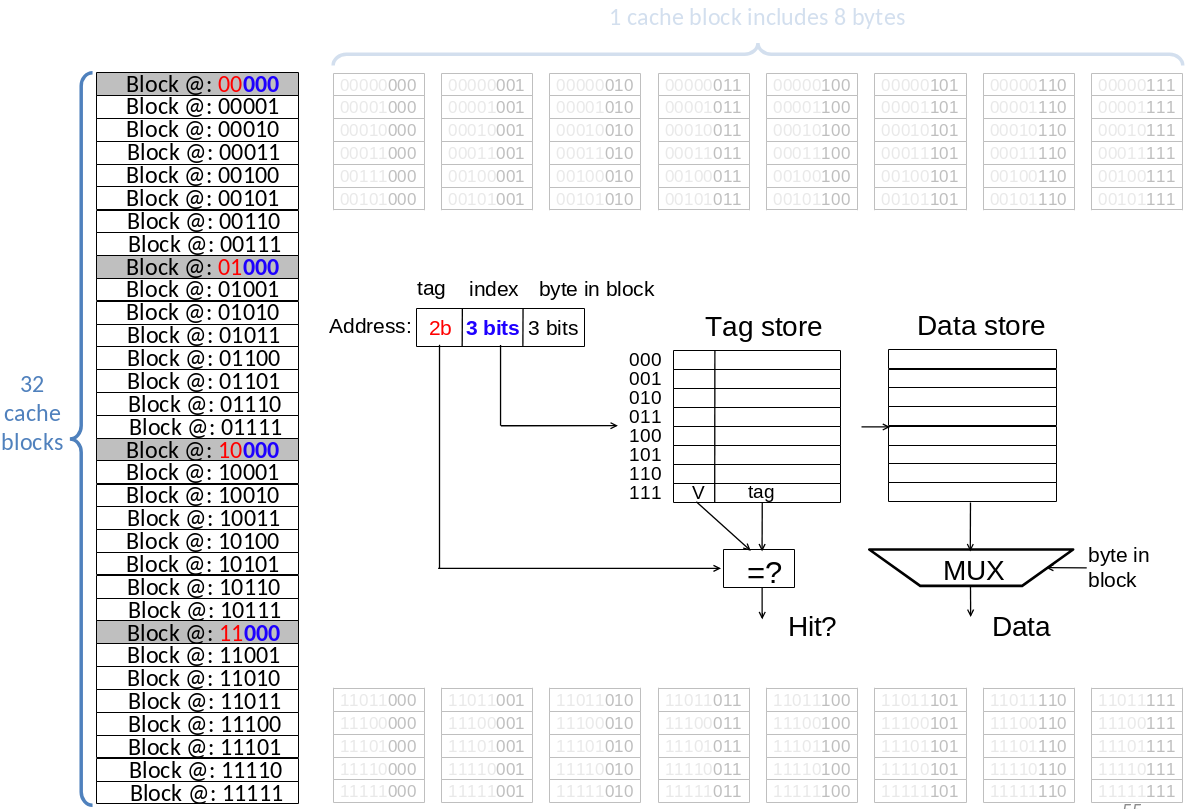
Set Associativity
Le Direct-mapped cache à un problème: En effet un index de tag store peut faire référence à deux blocs de mémoire différents.
Imaginons les variables A et B ayant des adresses différentes mais avec le même index, si dans notre programme on fait des A B A B A B A B …, on va se retrouver avec une variable qui va écraser l’autre dans le tag store à cause de leur index, ce qui mène à ne jamais faire de cache hit.
Pour éviter ce problème il est possible de répartir les entrées sur une autre colonne dans le cache pour écrire dedans si un ajoute une entrée ayant le même index.
Chaque colonne ayant moins de lignes on va donc réduire le nombre de bits pour définir l’index et augmenter celui du tag.
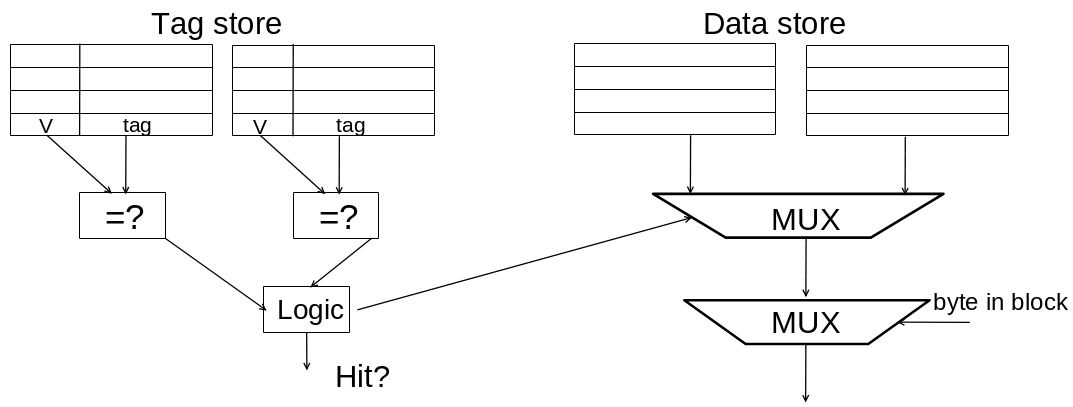
CEPENDAAAAAANNNNT
Quand on veut rajouter une entrée alors que toutes les colonnes d’un index sont utilisées on va remplacer la variable qui à été la moins récemment utilisée.
On peut même carrément faire de la full set associativity et ne plus avoir d’index en ayant de colonnes que la taille du cache le permet (on a donc plus que des bits pour désigner un tag et un bloc)
IMPORTANT
Il faut comprendre qu’un cache a une taille définie car sur une puce séparée, faire du set-associativity étale donc les index en colonnes. Il y a donc au final autant d’entrées entre du full set associativity et du Direct-mapped cache